
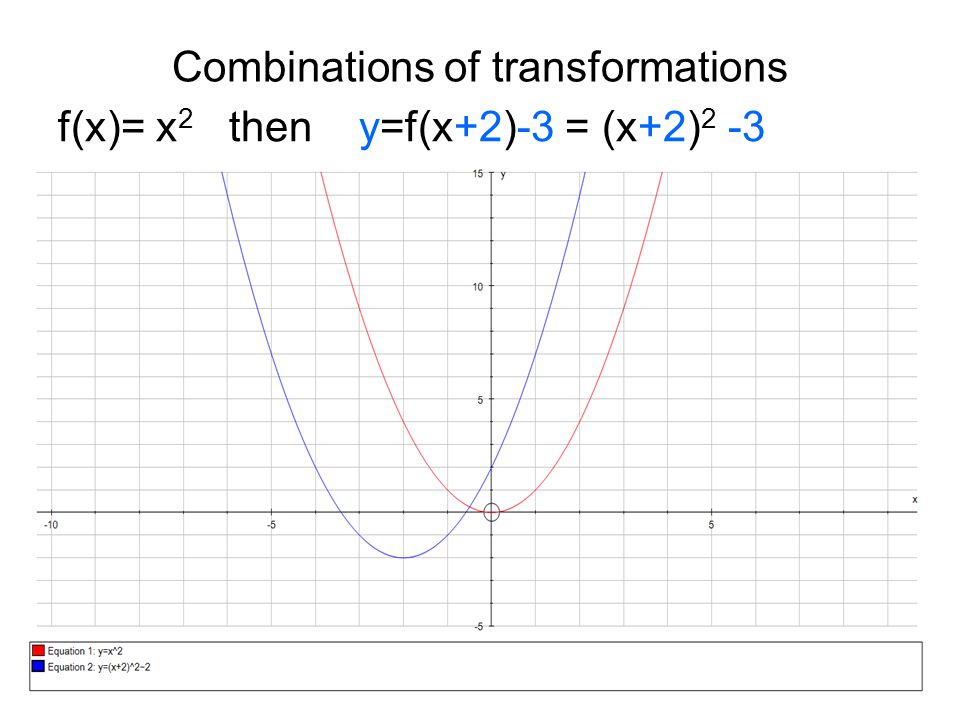
Describe The Transformations Of The Graph Of Y X That Will Produce The Graph Of Y X 2 2 3 Brainly Com
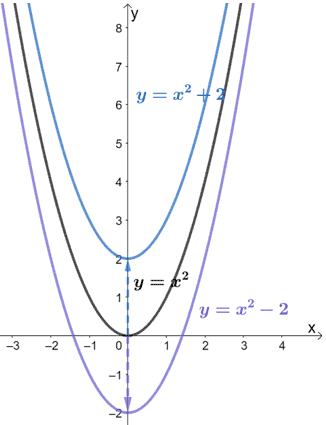
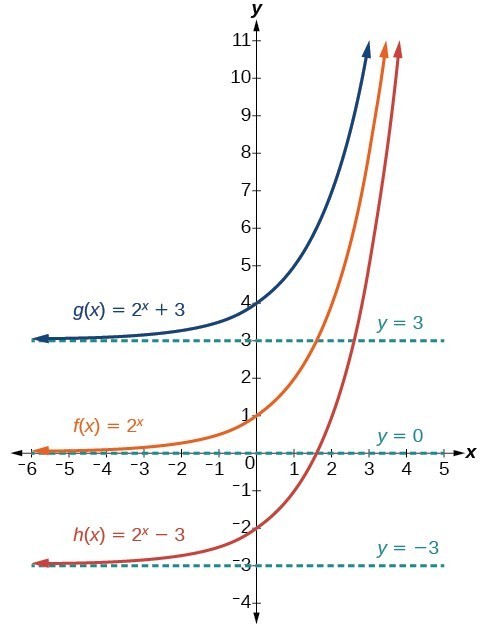
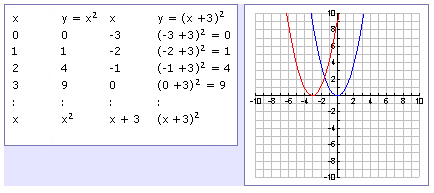
Move 2 spaces up h (x) = 1/x 2 Move 3 spaces down h (x) = 1/x − 3 Move 4 spaces right h (x) = 1/ (x−4) graph Move 5 spaces left h (x) = 1/ (x5) Stretch it by 2 in the ydirection h (x) = 2/x Compress it by 3 in the xdirection h (x) = 1/ (3x) Flip it upside down h (x) = −1/xThis type of transformation also retains the shape of the graph but shifts it either upward or downward Let's what happens if we shift y = x 2 two units upward and downward When we translate a graph two units downward, we subtract 2 from the output value, y Similarly, we add 2 to y when we translate it two units to the upward
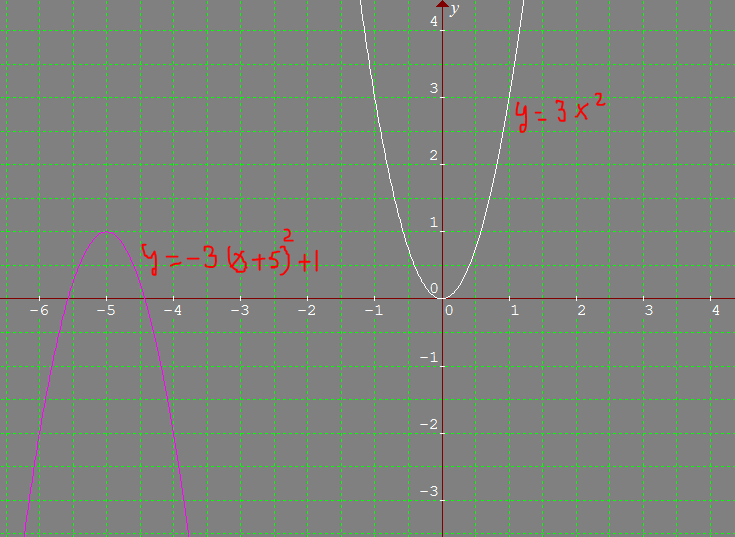
Y=(x+5)^2 transformation
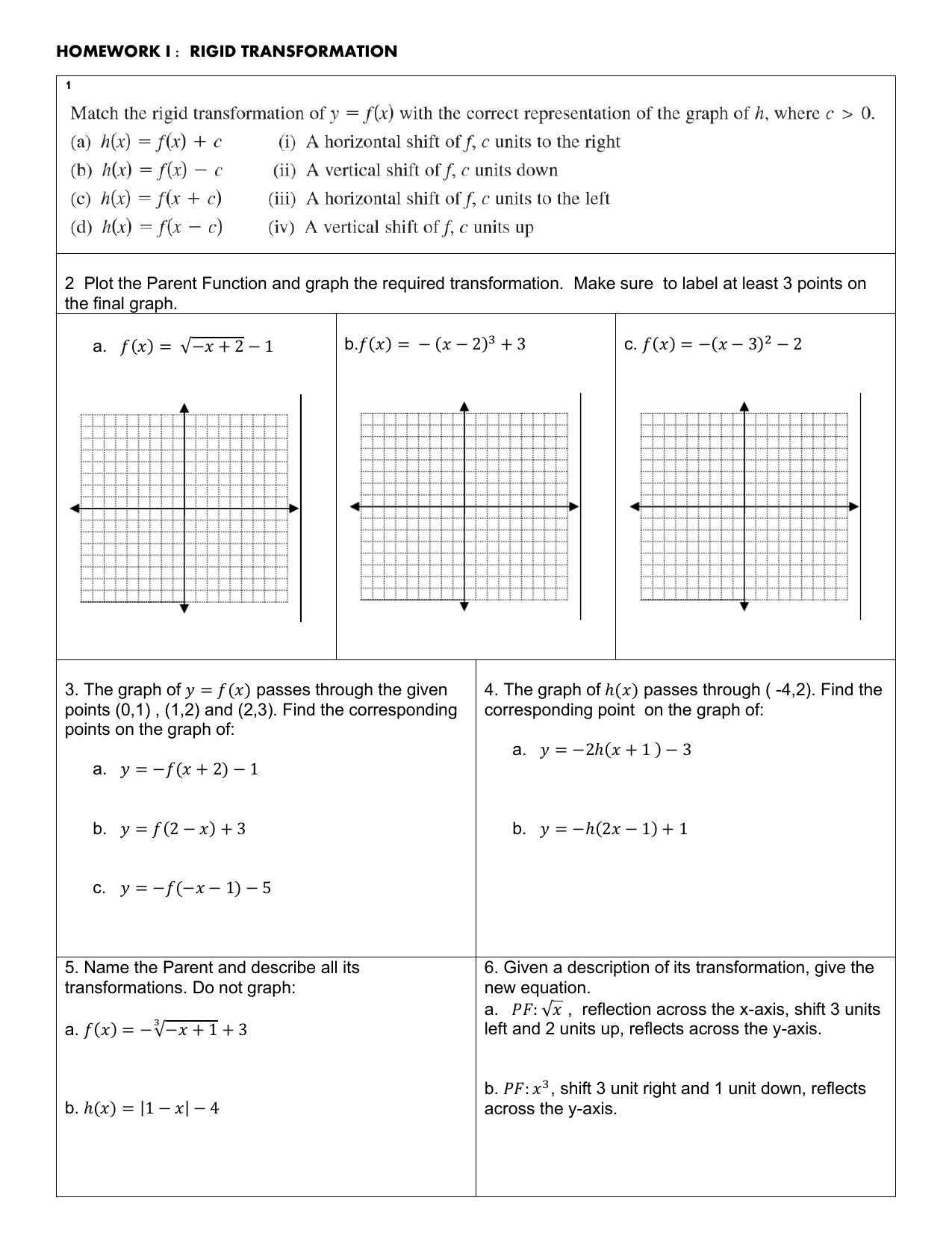
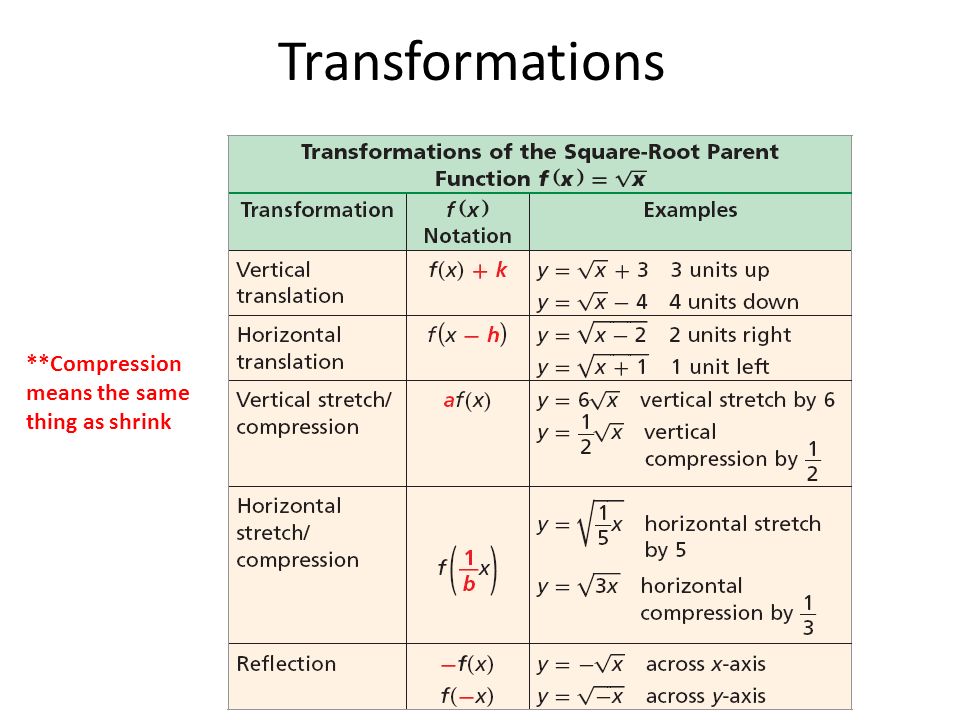
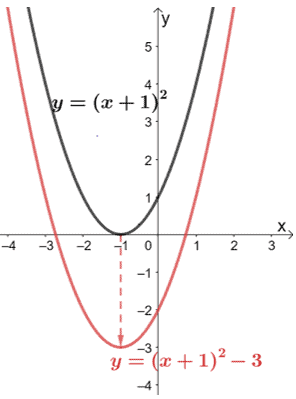
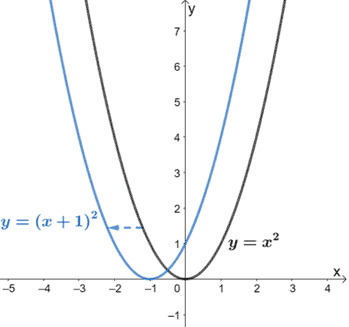
Y=(x+5)^2 transformation-This video explains how to determine the equation of an expoential function with a horizontal reflection and a vertical shifthttp//mathispower4ucom y=x^2 graph{x^2 10, 10, 5, 5} y=(x color(red)(3))^2 The graph shifts 3 units to the left graph{(x3)^2 10, 10, 5, 5} y=color(red)()(x3)^2 The graph is reflected over the xaxis graph{(x3)^2 10, 10, 5, 5} y=(x3)^2 color(red)(2) The graph is shifted 2 units down graph{(x3)^22 10, 10, 7, 3}
Discovering Advanced Algebra Resources
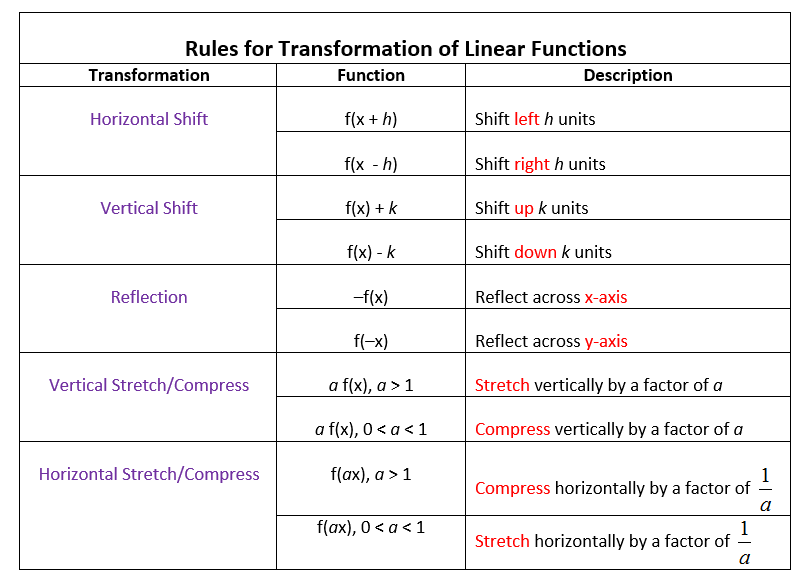
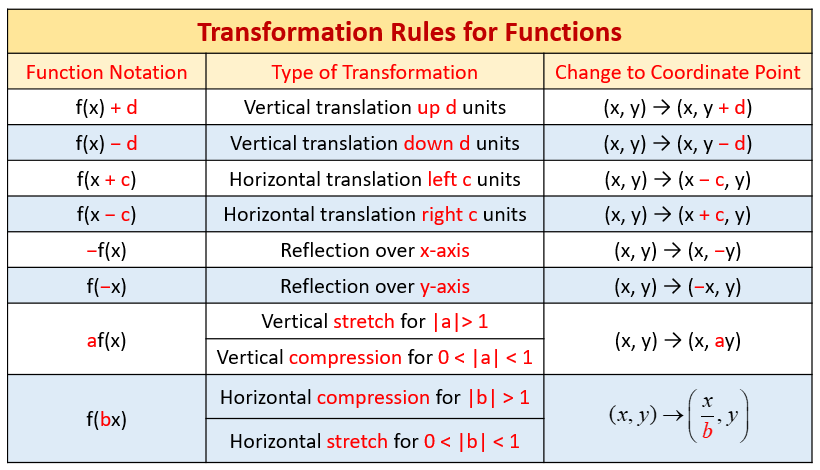
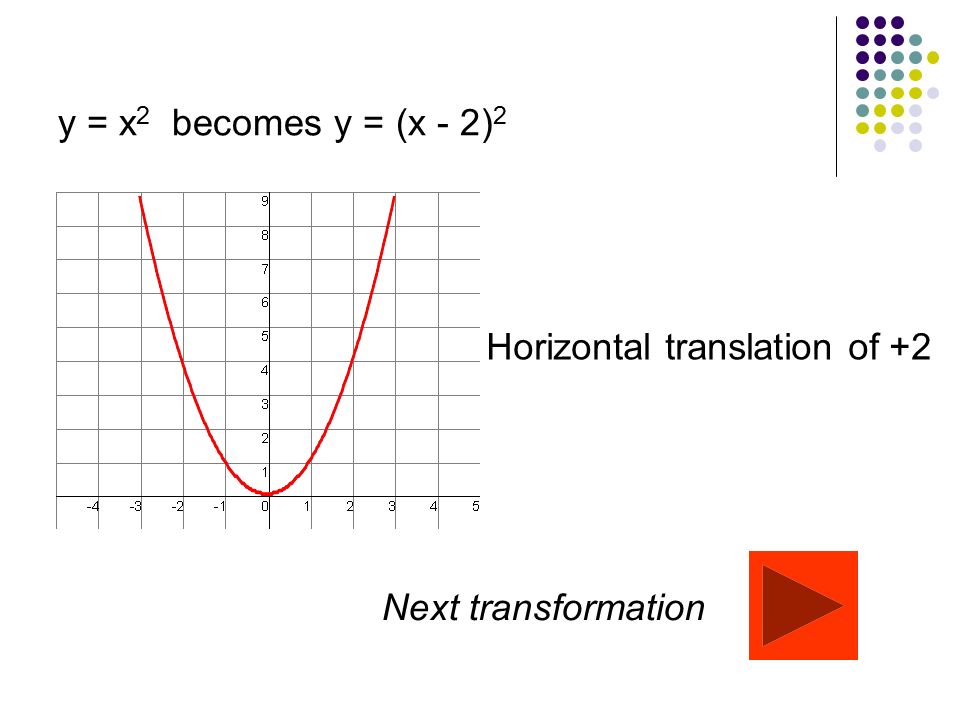
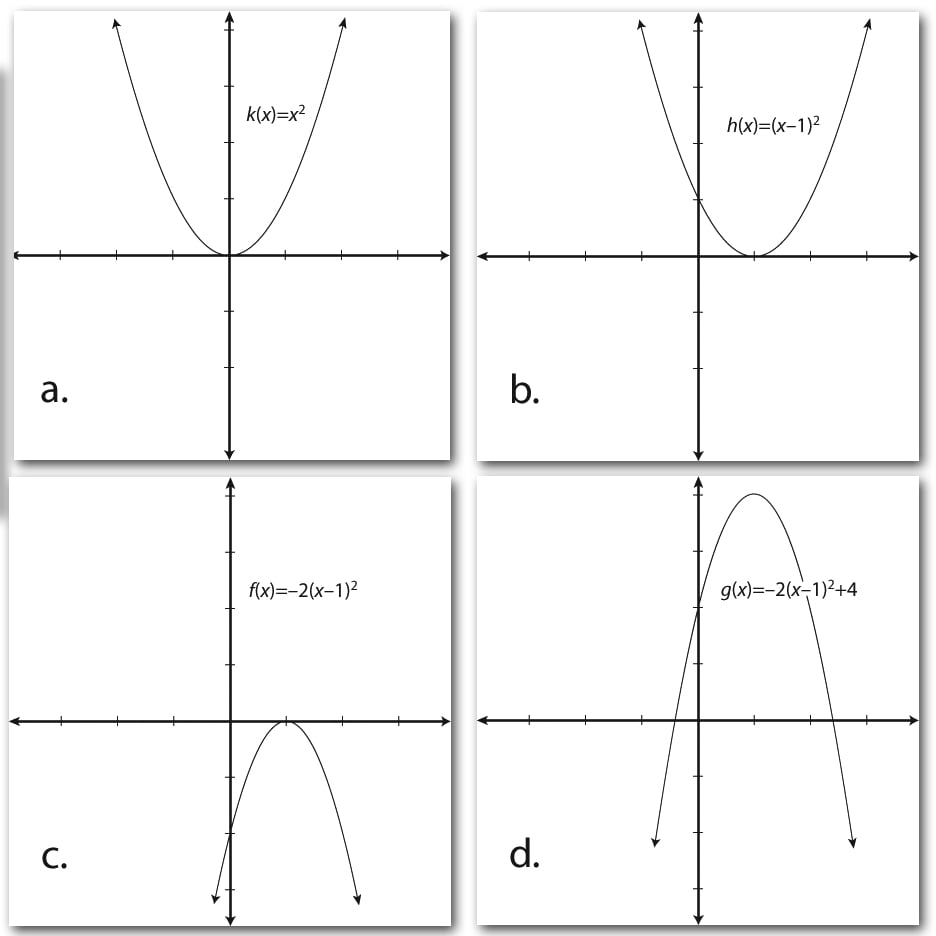
Describe the Transformation y=(2x)^2 The parent function is the simplest form of the type of function given Simplify Tap for more steps Apply the product rule to Raise to the power of For a better explanation, assume that is and is The transformation being described is from toAnd we loop through those points, making new points using the 2×2 matrix "a,b,c,d" for (let i = 0;Y = 3(x −2)2 1 y = 3 ( x 2) 2 1 The horizontal shift depends on the value of h h The horizontal shift is described as g(x) = f (xh) g ( x) = f ( x h) The graph is shifted to the left h h units g(x) = f (x−h) g ( x) = f ( x h) The graph is shifted to the right h h units
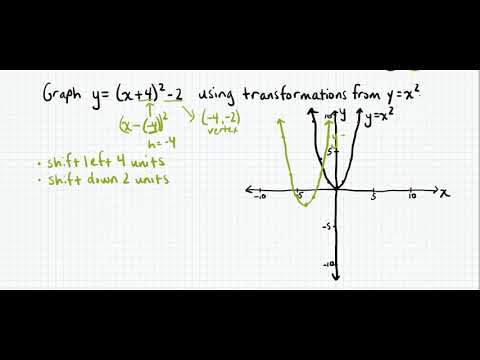
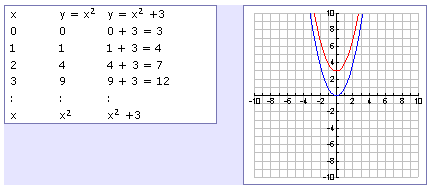
F ( x) = x2 A function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around For instance, the graph for y = x2 3 looks like this This is three units higher than the basic quadratic, f (xDescribe the Transformation y=x^22 y = x2 − 2 y = x 2 2 The parent function is the simplest form of the type of function given y = x2 y = x 2 For a better explanation, assume that y = x2 y = x 2 is f (x) = x2 f ( x) = x 2 and y = x2 − 2 y = x 2 2 is g(x) = x2 −2 g ( x) = x 2Y=X^2 Transformations Y=X^2 Transformations Log InorSign Up y = a bx − h 2 k 1 h = 0 2 k = 0 3 a = 1 4 b =
Y=(x+5)^2 transformationのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 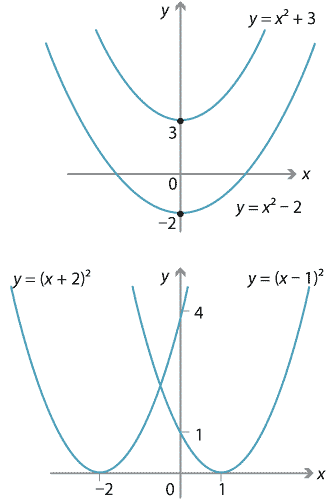 |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Y=(x+5)^2 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
$$ F_Y(y) = P(Y < y) = P(X^2 < y) = P(\sqrt{y} < X < \sqrt{y}) = \int_{\sqrt{y}}^{\sqrt{y}} f_X(t) \, dt $$ but since $f_X$ is defined piecewise, to proceed at this point we need to analyze several cases We already know that $F_Y(y) = 0$ if $y \leq 0$ and $F_Y(y) = 1$ if $y \geq 4$Factor a 1 1 out of the absolute value to make the coefficient of x x equal to 1 1 Factor a 1 1 out of the absolute value to make the coefficient of x x equal to 1 1 Find a a, h h, and k k for y = x−52 y = x 5 2 The horizontal shift depends on the value of h h
Incoming Term: y=x^2 transformations, y=x^2 transformations calculator, y=f(x+2) transformation, y=(x+5)^2 transformation, y=(x-3)^2 transformation, y=x^2-4 transformation, y=-(x-1)^2 transformation, y=x^2-7 transformation, transformations of y=x^2 parent parabola, y=a(x-h)^2+k transformations,




0 件のコメント:
コメントを投稿